プトレマイオス(トレミー, Ptolemaios, Ptolemy)の定理
#数楽トレミーの定理:円に内接する四角形の2本の対角線の長さの積は対辺の積の和に等しい。これは実は次のように書き直せます。公式:sin(α+β)sin(β+γ)=sin(α+β+γ)sin β+sin α sin γβ+γ=90°の場合がsinの加法公式です。
#数楽 一つ前のツイートの三つの角度に関するsinの加法公式(トレミーの定理を書き直したもの)はsinの通常の加法公式を特別な場合に含み、逆にsinの通常の加法公式から一つ前のツイートの三つの角度に関するsinの加法公式(本質的にトレミーの定理)を簡単に示せます。

#数楽 だから、トレミー(Ptolemy)の定理は実質的にsinの通常の加法公式と本質的に同等のことを言っているということになります。pic.twitter.com/q73s9xaMi4
#数楽 トレミーの定理は円に内接する四角形や三角形を扱っているので、トレミーの定理と三角函数の関係について語る場合には、正弦定理を前もって証明しておいて(易しい)、空気のごとく使うことにしないと苦しいです。
#数楽 トレミーの定理は21世紀になってからクラスター代数関係の数学に登場して結構活躍したので、21世紀になってからトレミーの定理の重要性を再認識した数学者は結構多いと思います。https://www.google.co.jp/search?num=100&q=("トレミーの定理"++OR+Ptolemy)+("クラスター代数"+OR+"cluster+algebras")&oq=("トレミーの定理"++OR+Ptolemy)+("クラスター代数"+OR+"cluster+algebras") …
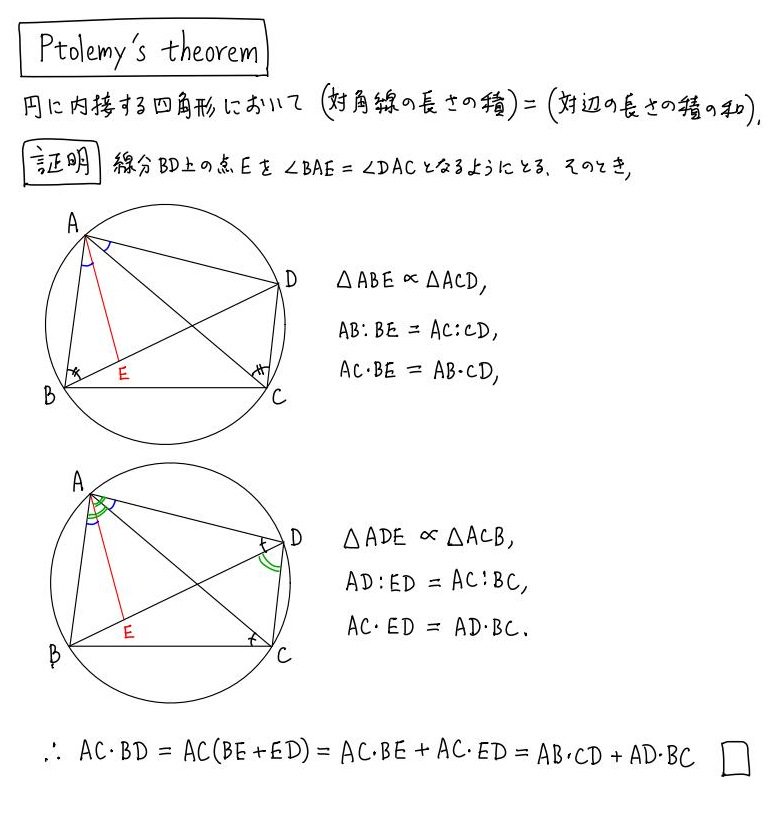
#数楽 私も21世紀になってからトレミーの定理の証明を勉強し直しました。添付画像をトレミーの定理のよく見る証明。すでに紹介したようにトレミーの定理からsinの加法公式が出ることは自明。トレミーの定理は実質的にsinの加法公式そのもの。pic.twitter.com/G23iGV0mr2
#数楽 トレミーの定理は xx'=yy'+zz'の形をしています。その形の公式で有名なものにはグラスマン多様体に関するプリュッカー関係式があります。だから行列式が関係して来る。様々な数学がそこに関係して来て、クラスター代数という21世紀初頭を代表する数学の一つになりました。
#数楽 以上のような21世紀の数学事情があるので、トレミーの定理は単にsinの加法公式と同等な定理とみなして終わりにするのではなく、それ自体が様々な数学を接合する特別な価値を持っていたと考えるべきだと思われます。トレミーさん=プトレマイオスさんもびっくりしていることでしょう。
プトレマイオスは『アルマゲスト』において実測値と理論値の整合性を確かめるために、三角比の値の正確な表を必要とした。そのために「トレミーの定理=sinの加法公式」を使い、小さな角度の三角比を求め、それを足していったのだ。つまりプトレマイオスは実際にこの定理を加法公式として使っているhttps://twitter.com/genkuroki/status/844078625607503874 …

#数楽 プトレマイオス(Ptolemy)さんによるトレミー(Ptolemy)の定理の使い方の解説のリンク(三角函数表を作るときに使った)https://en.wikipedia.org/wiki/Ptolemy%27s_table_of_chords …http://hypertextbook.com/eworld/chords/
#数楽 プトレマイオスさんによるトレミーの定理の使い方の解説https://books.google.co.jp/books?id=8eaHxE9jUrwC&pg=PA56&lpg=PA56&dq=Ptolemy+"table+of+chords"f#v=onepage&q=Ptolemy "table of chords"f&f=false …リンク先のp.58のFig.3.4がトレミーの定理の図。トレミーの定理は実質的に三角函数の加法定理として使用されている。
#数楽 プトレマイオスさんは自身の定理(トレミーの定理)を実質的に三角函数の加法定理として利用しましたが、トレミーの定理の「広い範囲の数学と関係している」(クラスター代数)という意味での重要性は三角函数の加法定理との関係にこだわると見えて来ないので要注意かも。
うげげげげ。「トレミーの定理」についてググると「トレミーの定理を大学入試で使ってよいのですか?」のようないつものくだらない質問が目立つな。日本の数学教育の闇だな、そういう傾向は。こっちは「プトレマイオスの三角函数表」や「クラスター代数」の純粋に面白い話だと思っているんだが。
#数楽 三角関数の加法定理はプトレマイオスの定理(トレミーの定理と英語を使いたくないw)と同値だが、プトレマイオスの定理を長方形に適用したものが三平方の定理になっている。長方形はそれに外接する円を持つ故、必ず適用できる。長方形を使ってα+β=90°の場合の加法定理が図示できる。
自分で描く文書では「トレミーの定理」とは決して書きません。「プトレマイオスの定理」と書きます。でも、「ユークリッド幾何」を「エウクレイデス幾何」と書く勇気はありません。
#数楽 個人的には、プトレマイオスの定理(トレミーの定理)は三角函数の加法定理よりもずっと広い数学と関係する話だと宣伝した方がよいと思う。プトレマイオスの定理経由の加法定理の証明は回転との関係も見難い。三角函数の加法定理は三角比の定義から直接かつ容易に示せ、回転との関係も見易い。
#数楽 大事なポイントは「三角函数の加法定理は難しい話だ」という感覚自体がひどい誤解だということ。プトレマイオスの定理(トレミーの定理)を使った巧妙な方法に目を奪われるとその辺を誤解する可能性がある。まあ、トレミーの定理も三角函数の加法定理も中学生レベルの超易しい話なのですが。
同意します。リア厨2のとき(クラスメートの兄から借りた)高校の数学2Bの参考書に同様の図があって(α、β、α+βがともに0からπ/2のときは)加法定理が成り立つことが納得できますた。 #数楽https://twitter.com/genkuroki/status/844354134773923840 …
#数楽 リンク先で紹介した「相対論的」プトレマイオス(トレミー)の定理の話の続き。リンク先のリンク先ではプリュッカー関係式に帰着する方法で証明していますが、みんなよく知っている平面幾何のトレミーの定理に帰着することもできます。続くhttps://twitter.com/genkuroki/status/844083062782619649 …

#数楽 続き。Pennerさんによる原論文 https://projecteuclid.org/euclid.cmp/1104160216 … 。添付画像はそのPennerさんの論文より。Pennerさんの論文のProp.2.6(a)のトレミー公式は平面上の通常のトレミーの定理からの直接の帰結として証明されます(Morin)。pic.twitter.com/A4EyRgcbJZ
#数楽 続き。まず3次元のミンコフスキー空間を考えます。内積は〈u,v〉=u_0 v_0 - u_1 v_1 - u_2 v_2 です。u=(u_0,u_1,u_2)に対して、u'=(u_1,u_2)と定め、u'の方での内積はいつもの内積だとしておきます。続く
#数楽 続き。そのとき||u'||=√(u_1^2+u_2^2).正のライトコーンをL^+={u|u_0=√(u_1^2+u_2^2)}と書くと、時刻が同じu,v∈L^+, u_0=v_0に対して、簡単な計算によって、〈u,v〉= ||u'-v'||^2/2.続く
#数楽 正のライトコーン上のベクトルu,v∈L^+に対して、λ(u,v)=√(u,v)とおく。もしもu_0=v_0ならばλ(u,v)=||u'-v'||/√2=(同一円周上の点u',v'の距離)/√2となるので、続く
#数楽 続き、a,b,c,d∈L^+, a_0=b_0=c_0=d_0で、a,b,c,dの順に同一円周上に乗っているとき、平面幾何のトレミーの定理より、λ(a,c)λ(b,d)=λ(a,b)λ(c,d)+λ(a,d)λ(b,c).続く
#数楽 続き。a,b,c,dのそれぞれを別々に正の実数倍しても、その等式は保たれるので、任意の正のライトコーン上の点a,b,c,d∈L^+が円周上に射影したときその順序に並んでいるとき、λ(a,c)λ(b,d)=λ(a,b)λ(c,d)+λ(a,d)λ(b,c).続く
#数楽 続き。これがPennerさんの論文(1987)のProp.2.6(a)のトレミー公式です。以上で採用したミンコフスキー空間の計量(内積)の符号が論文とは逆転していることには注意して下さい。平面幾何のトレミーの定理を知っていれば、高々大学1年レベルの話に過ぎません。続く
#数楽 続き。以上の話程度ならよくでいる中高生なら完璧に理解できると思います。そういうとても易しい話が実はとてつもなく役に立っています。21世紀になってから、クラスター代数の話と結びついて結構大きな話になっている。
#数楽 "プトレマイオス(トレミー, Ptolemaios, Ptolemy)の定理"https://twitter.com/i/moments/844444790636924931 …
#数楽 続き。以上の話は3次元ミンコフスキー時空のライトコーン上に自然にトレミーの公式が拡張されるという話。ライトコーンの内側には双曲面H: u_0^2=u_1^2+u_2^2が入っており、これをメトリック込みで単位円盤上に射影したものは、続く
#数楽 続き、異なる射影の仕方によって、ポアンカレディスクと呼ばれるものになったり、クラインディスクと呼ばれるものになったりします。負の定曲率の無限に広い世界が単位円盤内の有限の領域で表現される。リンク先の図が見やすいです。http://web1.kcn.jp/hp28ah77/jp3_poinc.htm …
#数楽 続き。単位円盤はケーリー変換で複素上半平面とも同一視できます。これらは様々な具体的で美しい数学の舞台になっています。そして、画家のエッシャーさんの有限の円盤内に描かれた無限の繰り返し模様の舞台でもあります。https://www.google.co.jp/search?q=�%82�ッシャー+繰り返し模様&hl=ja-jp&client=safari&tbm=isch&tbs=rimg:Cayfu8ARZ90WIqAB5QobXY1eShboTl7_1dlSULHdvepUwDW3htNdgzjQMJMNubc0FfcDvnoKZZE0XqPl4_1-xyUt5eq2mJotUQPT4u_1FCYjvyv6s984BoXaLeoAkgjJLQ_1JvfhBo0pvoOgcdf84Lhk7xHvCLq6c6nxEBubMyMaacV48htEy_1roIZlPzv1lrMZnO9nfo2um3pp_17oskefmU8Exx6QAhPrV_1T_1djgCoSCeUKG12NXkoWEW7776fsxkK4KhIJ6E5e_13ZUlCwRT7fV5G9oeRkqEgl3b3qVMA1t4RH1Wk6oYbWaaioSCbTXYM40DCTDEZpBLr7ln1P8KhIJbm3NBX3A754RDr4WNiDLelYqEgmCmWRNF6j5eBFAAyZdJknbHCoSCf_1sclLeXqtpEeeOZYU68JyFKhIJiaLVED0-LvwRs7YHWKNRQ4oqEglQmI78r-rPfBGPaPRUCRehrSoSCeAaF2i3qAJIEeRwuSVii8-YKhIJIyS0Pyb34QYR2kygrYZc3dcqEgmNKb6DoHHX_1BFOA45dRwvA2yoSCeC4ZO8R7wi6EZpBLr7ln1P8KhIJunOp8RAbmzMR7uoyljrlLxYqEgkjGmnFePIbRBEosA_1_1PUko1SoSCcv66CGZT879Eav5XUFRotqnKhIJZazGZzvZ36MR_1oiB9luo_16MqEglrpt6af-6LJBH-iIH2W6j_1oyoSCXn5lPBMcekAEdMz39N4kUaWKhIJIT61f0_13Y4ARbt_1Vo7KjDHg=&tbo=u&ved=0ahUKEwi8h_7rpurSAhVFnpQKHRCfDiMQuIIBCCo#imgrc=md1h9oxFNLNB3M …:
#数楽 円盤内に描かれたエッシャーさんによる無限の繰り返し模様を見ると、エッシャーさんは確実に単位円盤への離散群の作用を理解していたことがわかります。先のPennerさんによるトレミーの公式の拡張は、無限に広い単位円盤の境界とトレミーの定理を結び付けました。
#数楽 ポアンカレ単位円盤とその境界の話はさすがに高校レベルの話だとは言い難いです。しかし、健全な直観でかなりのところまで直観的に理解できそうな話がたくさんあるので、解説文をググって読んでみると楽しめるかもしれません。
#数楽 単位円盤上の幾何は負の定曲率の方の非ユークリッド幾何のモデルとしても有名です。曲率が負なせいで単位円盤内で少し離れた場所から同じ方向に同じ速さで平行にまっすぐに進んで行くと、互いにどんどん離れて行ってしまいます。その様子はエッシャーの作品を見てもわかります。
#数楽 エッシャーの作品を見れば、単位円盤内での「直線」(測地線)は境界に直交する円弧(極限としても直線を含むと考える)であることがわかります。https://www.google.co.jp/search?q=�%82�ッシャー+繰り返し模様&hl=ja-jp&client=safari&tbm=isch&tbs=rimg:Cayfu8ARZ90WIqAB5QobXY1eShboTl7_1dlSULHdvepUwDW3htNdgzjQMJMNubc0FfcDvnoKZZE0XqPl4_1-xyUt5eq2mJotUQPT4u_1FCYjvyv6s984BoXaLeoAkgjJLQ_1JvfhBo0pvoOgcdf84Lhk7xHvCLq6c6nxEBubMyMaacV48htEy_1roIZlPzv1lrMZnO9nfo2um3pp_17oskefmU8Exx6QAhPrV_1T_1djgCoSCeUKG12NXkoWEW7776fsxkK4KhIJ6E5e_13ZUlCwRT7fV5G9oeRkqEgl3b3qVMA1t4RH1Wk6oYbWaaioSCbTXYM40DCTDEZpBLr7ln1P8KhIJbm3NBX3A754RDr4WNiDLelYqEgmCmWRNF6j5eBFAAyZdJknbHCoSCf_1sclLeXqtpEeeOZYU68JyFKhIJiaLVED0-LvwRs7YHWKNRQ4oqEglQmI78r-rPfBGPaPRUCRehrSoSCeAaF2i3qAJIEeRwuSVii8-YKhIJIyS0Pyb34QYR2kygrYZc3dcqEgmNKb6DoHHX_1BFOA45dRwvA2yoSCeC4ZO8R7wi6EZpBLr7ln1P8KhIJunOp8RAbmzMR7uoyljrlLxYqEgkjGmnFePIbRBEosA_1_1PUko1SoSCcv66CGZT879Eav5XUFRotqnKhIJZazGZzvZ36MR_1oiB9luo_16MqEglrpt6af-6LJBH-iIH2W6j_1oyoSCXn5lPBMcekAEdMz39N4kUaWKhIJIT61f0_13Y4ARbt_1Vo7KjDHg=&tbo=u&ved=0ahUKEwi8h_7rpurSAhVFnpQKHRCfDiMQuIIBCCo#imgrc=md1h9oxFNLNB3M …:
#数楽 単位円盤は複素平面内で考えることが多いです。複素構造を考えることはちょうど「長さを忘れて角度の情報だけを残すこと」に一致しており、複素構造だけでも面白いことをたくさん言えるからです。複素平面で幾何をやると直線と円が仲間になってしまうのは長さを忘れたからです。
#数楽 トレミー(プトレマイオス)の定理の複素平面を使った証明もよく見かけます。「複素平面上の4点について、非調和比(複比)が実数になることと同一円周もしくは同一直線に乗ることは同値である」という結果と三角不等式の等号成立条件を使うとトレミーの定理の逆も示せます。
#数楽 任意の複素数a,b,c,dについてトレミー型の公式(a-c)(b-d)=(a-b)(c-d)+(a-d)(b-c)が成立しています。次も無条件で成立。三角不等式より、|a-c||b-d|≦|a-b||c-d|+|a-d||b-c|.続く
#数楽 続き。三角不等式の等号が成立しているなら、(a-c)(b-d)、(a-b)(c-d)、(a-d)(b-c)が0から出る同一の半直線上に乗ります。そのとき、a,b,c,dの複比は実数になるので、4点は同一円周上の乗ります。これで複比の応用でトレミーの定理の逆を示せた。
#数楽 平面幾何のプトレマイオス(トレミー)の定理は三角函数の加法定理と実質的に同じことを述べている易しい結果なのですが、三角函数の加法定理のイメージではとらえることができない側面を持ち、数学の諸分野と広く関わりあっている面白い数学的結果だと思います。
#数楽 https://twitter.com/genkuroki/status/844551665525022720 …リンク先では3次元ミンコフスキー空間内の正時刻のライトコーン上にトレミー(プトレマイオス)の定理が拡張されるという話をしたのでした。そして、ライトコーンはポアンカレディスク(複素平面の単位円盤)の境界に射影される。続く
#数楽 続き。だから、正のライトコーン上のトレミーの定理は単位円盤の境界(円周)上のトレミーの定理の拡張になっているわけです。正のライトコーンは位相的には(円周)×{正の実数全体}です。正の実数部分が何を意味しているかもわかっています。それはホロサイクルを指定するパラメーター。
#数楽 続き。ホロサイクルという専門用語を使いましたが、素朴な定義であれば小学生でも理解できます。「単位円盤 X^2+Y^2<1 に含まれる円で境界に接するもの」をホロサイクルと呼ぶ。たったこれだけ。リンク先に見やすい図があります。http://web1.kcn.jp/hp28ah77/jp15_horo.htm …
#数楽 3次元ミンコフスキー空間の座標を (t,x,y) と書いて、点(-1,0,0)と(t,x,y)を結ぶ直線と平面t=0の交点を(0,X,Y)と書くことにします(t軸を上方向に取る習慣で図が描かれることが多い)。すなわち、X=x/(t+1)、Y=y/(t+1)。続く
#数楽 続き。その対応によって正の双曲面t^2=x^2+y^2+1, t>0上の点は単位円盤X^2+Y^2<1内の点と一対一に対応します。正のライトコーンt^2=x^2+y^2, t>0上の点(a,b,c)を任意に取ります。これがホロサイクルをどのように定めるか?続く
#数楽 続き。正のライトコーン上の点(a,b,c)はat-bx-cy=1によって、平面を定めます。その平面と正の双曲面t^2=x^2+y^2+1の共通部分を単位円盤内にうつすと境界に接する半径1/(1+a)円になる。そしてそのことは高々高校レベルの数学で容易に確認できます。続く
#数楽 続き。必要ならt軸について回転することによって、計算はa=b>0,c=0の場合だけ実行すれば十分。t^2-1=x^2+y^2とt-x=1/aの仮定のもとでX=x/(t+1),Y=y/(1+t)とおくと、(X-(a/1+a))^2+Y^2=1/(1+a)^2となる。
#数楽 続き。(X-(a/1+a))^2+Y^2=1/(1+a)^2が正のライトコーン上の点(a,a,0)が定める単位円盤内のホロサイクルの方程式。この手のことを知っていればPennerさんの論文 https://projecteuclid.org/euclid.cmp/1104160216 … を読み易くなると思う。
#数楽 訂正。括弧の位置がずれた。正のライトコーン上の点(a,a,0)が定める単位円盤内のホロサイクルの方程式は、正しくは(X-a/(1+a))^2+Y^2=1/(1+a)^2です。
紙に手書きではなく、タブレット端末で手書きも強力なのですが、面積的にひどく狭いので、紙とは違う使い方をしないとメリットは小さい。切り貼りを気軽にできる点はべんり。実際に私がタブレットPCでとったノートの実例が次の場所にある→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/201205Nagao/ …
#数楽 タブレット端末で数学の手描きのノートをとった実例としてよく紹介している http://www.math.tohoku.ac.jp/~kuroki/LaTeX/201205Nagao/ … のhttp://www.math.tohoku.ac.jp/~kuroki/LaTeX/201205Nagao/2012-05-09 Lecture 2 of Nagao, Kentaro.pdf …に「λ距離に関するPtolemyの定理」の話がある。上半平面で説明してあった。
#数楽 単位円盤では境界の円周状の点は無限遠にある。だから境界上の点を結ぶ測地線の長さは無限大になり、境界上の点のあいだの「距離」をそれらを結ぶ測地線の長さで測ることはできない。しかし、ホロサイクルで測地線を切れば有限の長さになるので、ホロサイクル間の「距離」なら測れる。続き
#数楽 続き。その方法で測ったホロサイクル間のλ距離にPtolemyの定理が拡張される。中学生レベルのユークリッド的トレミーの定理はホロサイクルのサイズを揃えた場合にちょうどなっており、その場合に一般の場合の証明は帰着する。
#数楽 ジーナスgの閉曲面にs個の穴が空いたものを考える(定曲率-1とする)。そこに穴から出発して穴で終わる測地線の切れ目を6g-6+3s本入れて切って、4g-4+2s枚の三角形に分割できます。大雑把に言うと、切り方を変える操作がPtolemyの定理で記述される。



